Getting trouble while solving math problems because you don’t know what is an even function? Leave the worries behind, here we will tell you everything about the even functions that will help you to solve the even functions queries very easily. You will come to know about the definition, calculation, difference, and many other things of even functions. We have explained in a very simple and easy way about every concept of what is even function related with.
What Is An Even Function?
The even function is called even if for all x values of the function f(x) is equal to f(−x). In other words, since the graph is symmetrical along the y-axis, the even functions have similar images.
Definition Of An Even Function
- Graphically the function is even can be defined as:
Even function can be defined as, a function f is even if concerning the Y-axis, the graph of f is symmetrical.
- Algebraically the function is even can be defined as:
Function f is, algebraically even, if and only if f(-x) = f(x) in the domain of f for all possible x values.
Even Function Example
Below we have an example on an even function so you will come to know more:
f(x) = x4 – 16
If we substitute x with -x,
Then, f(-x) = (-x)4 – 16 = x4 – 16
And if changing x to -x does not change the function’s value. Since f(-x) = f(x) the function is even.
What Is An Even Function Symmetry?
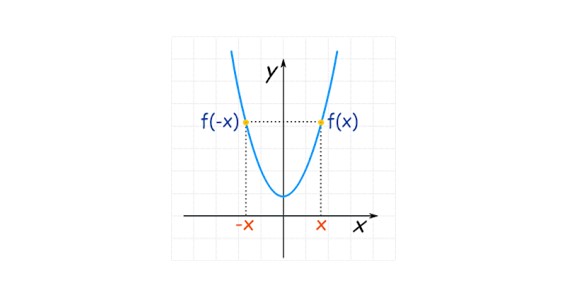
Even function symmetry can be explained in terms of graphs. Geometrically, concerning the y-axis, the graph of an even function is symmetrical, meaning that the graph appears unchanged until reflection on the y-axis. For opposite values, and even function can provide a similar or identical image.
Example of even functions is as follows:
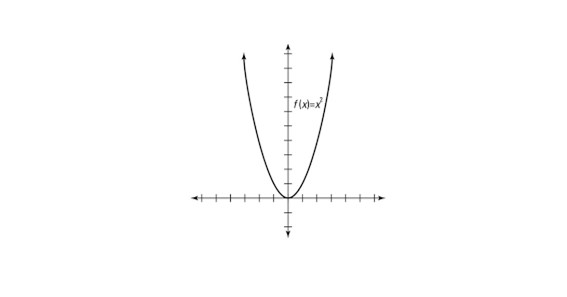
f(x) = x2 is an even function.
Even Function Formula
You can calculate the even function by using the formula as follow.
A function is even if the equality
f(x) = f(−x) and it is true for all x from the domain of definition.
Even Function Graph
The graph of even function is symmetrical. Even function graphs have or produce identical and similar images.
How To Tell If The Function Is Even Or Odd?
If you want to tell or know whether the function is even or odd it is simple. You need to substitute the f(x) = f(−x) and then further simplify the function. Algebraically, if you get the same function at the end then the function is even, if not then it is an odd function.
Below we have simplified it for you with a good example so you will understand it in a fast way.
Let’s determine whether the function f (x) = –6x2 + 8 is even, odd, or neither.
So let us substitute x to -x, in the above function and simplify it further:
f (–x) = –6(–x)2 + 8
= –6(x2) + 8
= –6x2 + 8
Hence, the function f(x) is even in the above example.
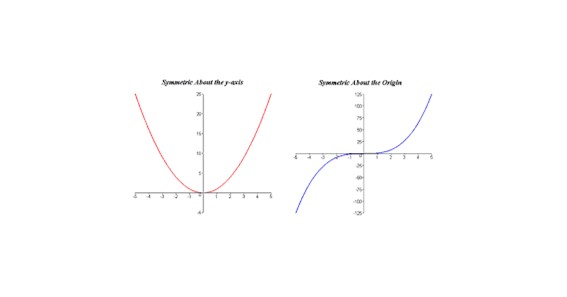
How To Identify Function Is Even Or Odd By The Graph?
Below we have explained the graph and from that, you will get help for how to tell if a function is even or odd from a graph. The graph is symmetrical along the y-axis if the equation is even. The graph is symmetrical to the origin if the function is odd.
What Is An Even Function Of t?
The even function of t is a periodic function. If a periodic f(t) function is an even function. The fact that the even function t that is f(t) can only have cosines in its Fourier series. Similarly, Fourier, the odd function sequence can contain only sines.
A function f(t) is called even if equation f(−t) = f(t) for all t values.
What Is An Even Degree Function?
A polynomial of the kth degree, p(x), is said to have an even degree polynomial function if k is an even number and if k is an odd number, an odd degree.
Notice that even if p(x) has a degree. It is not always a function that can be even. Also if p(x) has an odd value, it is not an odd function.
What Is An Even Root Function?
An even root function for a positive integer where n is greater than 1 and having even values. A root function is a function expressed by x1/n. If n is having the even values like 2,4,6,8….. Then it is called as Even Root Function.
What Is An Even Odd Function?
F(x) = 0, defined for all real numbers, is the only function that is both even and odd. There is just a line on the x-axis that lies on it. If you count equations that in terms of y are not a function, So x=0 will be both even and odd and it is just a line on the y-axis.
What Is An Even Monomial Function?
The monomial even function is that there is only one concept in the algebraic function and that it cannot consist of negative power. The function is even monomial if it has an even degree.
What Is An Even Polynomial Function?
If the degree of a polynomial f(x) is equal and the coefficient of lead is positive, then f(x) is equal to x ± ∞.
If function f(x) is an even polynomial of an even degree with a negative leading coefficient, then f(x) = ∞ , as x ± ∞.
What Is the Product of Even Function and Odd Function?
You will get an odd function as a product when you multiply an even function and an odd function.
The quotient is even of two even functions, and the quotient is even of two odd functions.
Special Properties Of Even Function
Below we have given some special properties that even functions have in terms of Adding and Multiplying:
- Addition:
- The sum algebraically of the two even functions is even
- A sum of an even and odd function is not even and not odd (Except where one function is zero).
- Multiplication:
- When two even functions are multiplied their product is also an even function.
- When an even function and an odd function multiplied their product is an odd function.
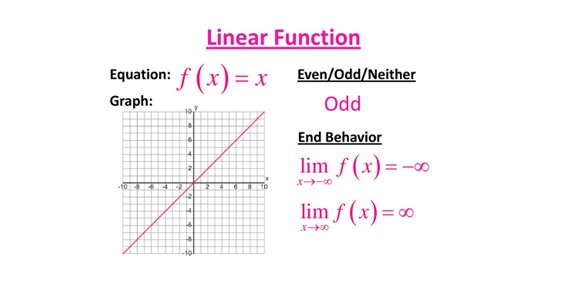
Is A Linear Function Even Or Odd?
A linear function is odd if the linear graph goes through the origin. The linear function is even if the graph does not go through the origin.
Can A Function Be Both Even And Odd?
F(x) = 0, defined for all actual numbers, is the only function that is both even and odd. It is just a line that is lying on the X-axis. If you count equations that in terms of y are not a function, so x=0 will therefore be both even and odd and is just a line on the y-axis.
FAQ
How Do You Know If A Function Is Even Or Odd?
You can know if a function is even or odd by determining it in an algebraic manner. You take the function and substitute the x in for -x to do so, and then simplify the equation further. If you end up with the very same function which you began with. That is if f(x) = f(-x) with all the signs being identical then the function is called even. And for odd function after substituting, the f (–x) = –f (x). Other than this criterion the functions are neither even nor odd.
What Does An Even Function Mean?
An even function means a function that has an exact even product after the substitution and graphically the function has symmetry.
What Does An Even Function Look Like?
Concerning the y-axis or along with the vertical line x = 0, the graph of an even equation is symmetrical. Note that the feature graph is divided uniformly on the y-axis and each half is an exact mirror of the other.
Is An Even Function Symmetric To The Y Axis?
Yes, an even function is symmetric to the Y axis. If the graph is symmetrical concerning the y-axis, a function is considered to be an even function.
What Are Even Functions?
The even function is called even when the: f(x) is equal to f(−x) for all x values. In other words, the even functions have identical images when the graph is symmetrical about the y-axis.
What Basic Functions Are Odd?
Odd Functions: The identity function, the cubing function, the reciprocal function, the sine function.
Which Of The 12 Functions Are Even?
Even Functions: The squaring function and the absolute value function. Odd Functions: The identity function, the cubing function, the reciprocal function, the sine function. Neither: The square root function, the exponential function and the log function.
What Is The Difference Between An Odd And Even Function?
The terms even and odd are used to describe a function’s symmetry. An even function is symmetric around a graph’s y-axis. An odd function is symmetric about the graph’s origin (0,0). This means that rotating an odd function 180 degrees about the origin will give you the same function you started with.
What Are 5 Examples Of Odd And Even Numbers?
What are odd and even numbers with examples? Odd numbers are those numbers that cannot be divided into two equal parts, whereas even numbers are those numbers that can be divided into two equal parts. Examples of odd numbers are 3, 5, 7, 9, 11, 13, 15,… Examples of even numbers are 2, 4, 6, 8, 10, 12, 14,.
Are All Absolute Functions Even?
By definition, a function f(x) is even if f(−x)=f(x) , and it is odd if f(−x)=−f(x) . So in the case of the absolute value function, it is clear that f(−x)=f(x)∀x∈R and hence it is an even function
Conclusion
Above we read about what is an even function? And you came to know about various things. You learned about even function, its definition, example, etc. You came to know about the even function in graphs and algebraic expressions. Questions like how the even functions are different from the odd functions? how to solve them even function? All this you learned from this article on what is an even function.